, Hisayoshi Muramatsu

概要

本研究紹介は村松が提案した準周期外乱オブザーバ（論文[H. Muramatsu, IEEE TCST, 2025] ）の理解・設計・実装を助ける大枠について解説する．準周期外乱オブザーバを一言で説明すると，現実によくある「ゆらぎをもつ周期外乱」を高精度に推定・補償可能な制御アルゴリズムである．論文はオープンアクセスになっており，無料で気軽に読むことが可能である．詳細について興味があれば，ぜひ読まれたい．

Hisayoshi Muramatsu, “Quasiperiodic Disturbance Observer for Wideband Harmonic Suppression,” IEEE Transactions on Control Systems Technology, Early Access, 2025.
[IEEE Xplore (Open Access)], [DOI:10.1109/TCST.2025.3566560], [Research Gate]

> BibTex

@ARTICLE{Muramatsu2025TCST,
author={Muramatsu, Hisayoshi},
journal={IEEE Transactions on Control Systems Technology},
title={Quasiperiodic Disturbance Observer for Wideband Harmonic Suppression},
year={2025},
volume={},
number={},
pages={},
doi={10.1109/TCST.2025.3566560}}

周期外乱

周期外乱は厳密に

\begin{align} d(t) = d(t-T) \end{align}

を満たし，制御精度を悪化させる外乱である．例えば，強制振動，トルクリップル，電流リップルらが周期外乱として存在する．他にも，産業機械をはじめとした繰り返し動作を行うロボット・自動機械に生じる繰り返し的な摩擦，姿勢変化，モデル化誤差は周期外乱となる．これら周期外乱はフーリエ級数により，

\begin{align} x(t)=\frac{a_0}{2}+\sum_{n=1}^\infty[a_n\cos(n\omega_0t)+b_n\sin(n\omega_0t)] \end{align}

のように表すことも可能である．すなわち，周期外乱とは必ずしも単一周波数のみを有する正弦波や余弦波ではなく，DC成分（$a_0/2$）と整数倍の周波数（$n\omega_0$）を持つ高調波も含みうる．

ここで一つの問題がある．周期外乱を取り扱う多くの従来研究は，現実の外乱が$d(t) = d(t-T)$を満たすと仮定している．しかし，現実の現象が，サイクルごとに全く同じ値をとることなどあるのだろうか？あったとして，「おおよそ同じ」値をサイクルごとにとるくらいであろう．すなわち，程度の大小はあれど，現実の現象がもつ周期性は，そのほとんどが「準周期的」であり，厳密に$d(t) = d(t-T)$を満たすことはまずない．

準周期外乱

上述した周期外乱の問題に対して，論文[H. Muramatsu, IEEE TCST, 2025] は周期ごとに多少の変動を許容するような「準周期外乱」を定義した．この準周期外乱の定義は，村松が過去の研究 [H. Muramatsu, Automatica, 2022] で提案した新たな準周期関数の定義に基づく，独自の定義である．そして「多少の変動」として，サイクルごとに分離周波数$\rho$より低周波に変化する外乱が準周期外乱として定義される（周期外乱はサイクルごとに一定）．分離周波数はハイパーパラメータであり，どの程度の変化を準周期性として許容するか，定義をチューニングすることが可能である．

この新たに定義された準周期外乱は，周期外乱も包括しており（$\rho=0$のケース），分離周波数に応じたサイクルごとのゆらぎも許容する．これにより，現実のサイクルごとに「おおよそ同じ」値をとり，これまで周期外乱として雑にモデル化されていた外乱を準周期外乱として適切にモデル化することが可能となる．すなわち，準周期外乱は周期外乱に比べ，実用性の高い定義となっている．

論文[H. Muramatsu, IEEE TCST, 2025] は，この準周期外乱を推定・補償する「準周期外乱オブザーバ」を提案している．

準周期外乱オブザーバ
Quasiperiodic Disturbance Observer（QDOB）

準周期外乱オブザーバのブロック線図は以下のようになる．

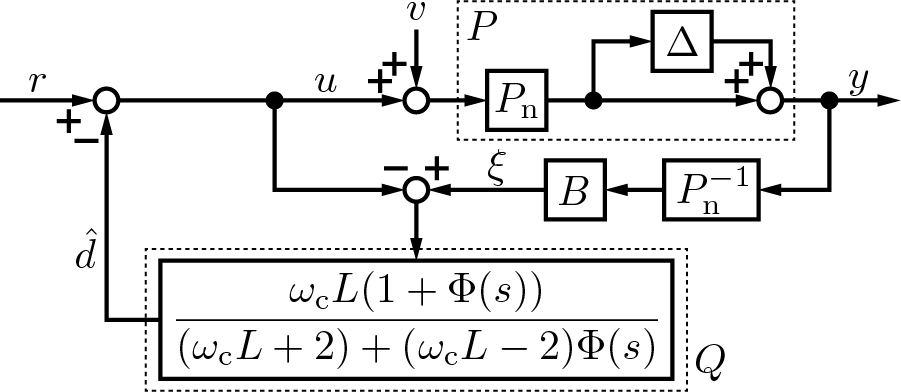
準周期外乱オブザーバは以下に定義される外乱$d$

\begin{align*} \mathcal{L}[d(t)]=\mathcal{L}[v(t)]+\Delta(s)\mathcal{L}[u(t)+v(t)] \end{align*}

を$\hat{d}$として推定し，これをフィードバックすることで補償する．外乱は外因信号$v(t)$のみならず，モデル化誤差を通した入力信号の影響$\Delta(s)\mathcal{L}[u(t)+v(t)]$も含まれている．すなわち，参照信号$r$がもつ周期性がモデル化誤差を通して励起する準周期外乱も推定・補償可能である．準周期外乱オブザーバを単一のフィードバックを有する形で，以下のように等価に描くこともできる（機能的には全く同じ）．

各，伝達関数やパラメータについて説明する．$P(s)$はプラントであり，公称モデル$P_n(s)$とモデル化誤差$\Delta(s)$を含んでいる．$B(s)$は一次のローパスフィルタ

\begin{align*} B(s)=\frac{\omega_{\mathrm{b}}}{s+\omega_{\mathrm{b}}} \end{align*}

である． $Q(s)$は外乱オブザーバの特性を決めるQフィルタと呼称されるフィルタであり，準周期外乱オブザーバは，村松が過去に提案した周期／非周期分離フィルタの周期通過フィルタ [H. Muramatsu, Automatica, 2022] と零位相ローパスフィルタを統合したフィルタをQフィルタに採用している．フィルタ$\Phi(s)$が周期通過フィルタのむだ時間と零位相ローパスフィルタを統合した線形位相ローパスフィルタである．

既存の外乱オブザーバと異なるユニークな構造として，１次ローバスフィルタ$B(s)$が逆公称モデル$P_n^{-1}(s)$にのみ付いており，$B(s)P_n^{-1}(s)$は厳密にプロパーでない（バイプロパー，もしくはプロパーでない）伝達関数となる．そして，Qフィルタはローパス特性を持たない． Qフィルタの$L$は準周期外乱の周期であり，$\omega_c$は先述した準周期外乱の定義にて登場した分離周波数$\rho$により以下のように決まるカットオフ周波数である．

\begin{align*} \omega_\mathrm{c}=\frac{2}{L}\tan{\left(\frac{L}{2}\rho\right)} \end{align*}

周波数特性

Qフィルタの周波数特性は以下となる．

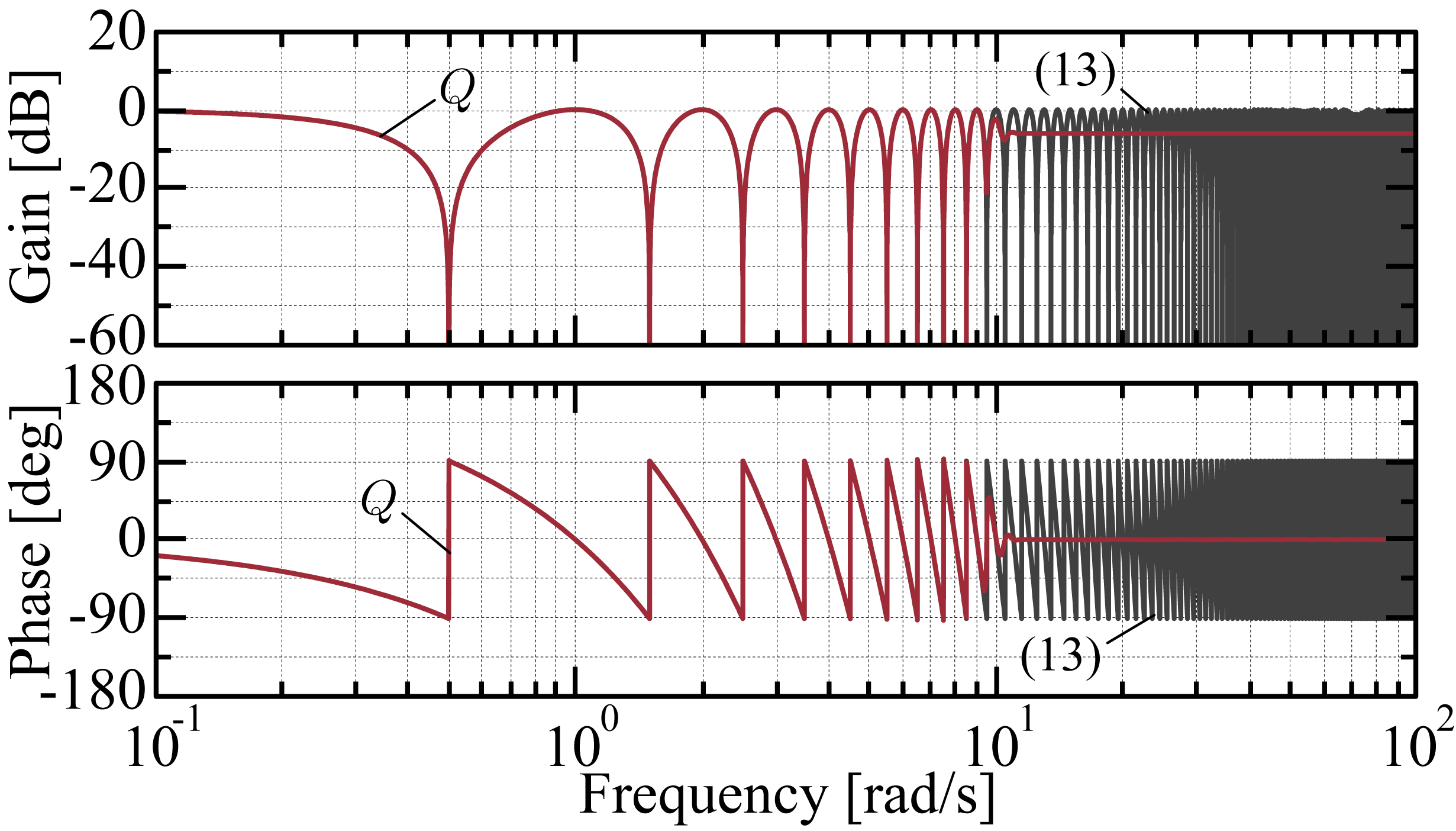
(13)は村松が過去に提案した周期／非周期分離フィルタの周期通過フィルタがもつ周波数特性である．そこへ，先述したように，零位相ローパスフィルタを統合することで，零位相ローパスフィルタのカットオフ周波数$\omega_{\mathrm{a}}$を超える周波数でバンドストップ（ノッチ）特性が減衰するように設計されている．そして，外乱抑圧特性にあたる感度関数$S(s)$と，ロバスト安定性の目安となる相補感度関数$T(s)$は，以下のような周波数特性になる．

この周波数特性には異なる傾向を示す３つの領域がある．まず，カットオフ周波数$\omega_{\mathrm{a}}$以下の周波数において，感度関数$S$が複数のバンドストップ特性により高調波とその周辺外乱を準周期外乱として抑圧する．次に，$\omega_{\mathrm{a}}<\omega<\omega_{\mathrm{b}}$の周波数が中間領域となる．最後に，$\omega_{\mathrm{b}}$以上の周波数において，相補感度関数$T$がロバスト安定性のためのローパス特性をもつ．

分離周波数$\rho$はカットオフ周波数$\omega_c$を通して，感度関数$S(s)$が有する複数のバンドストップ特性の帯域幅を以下のように調整できる．

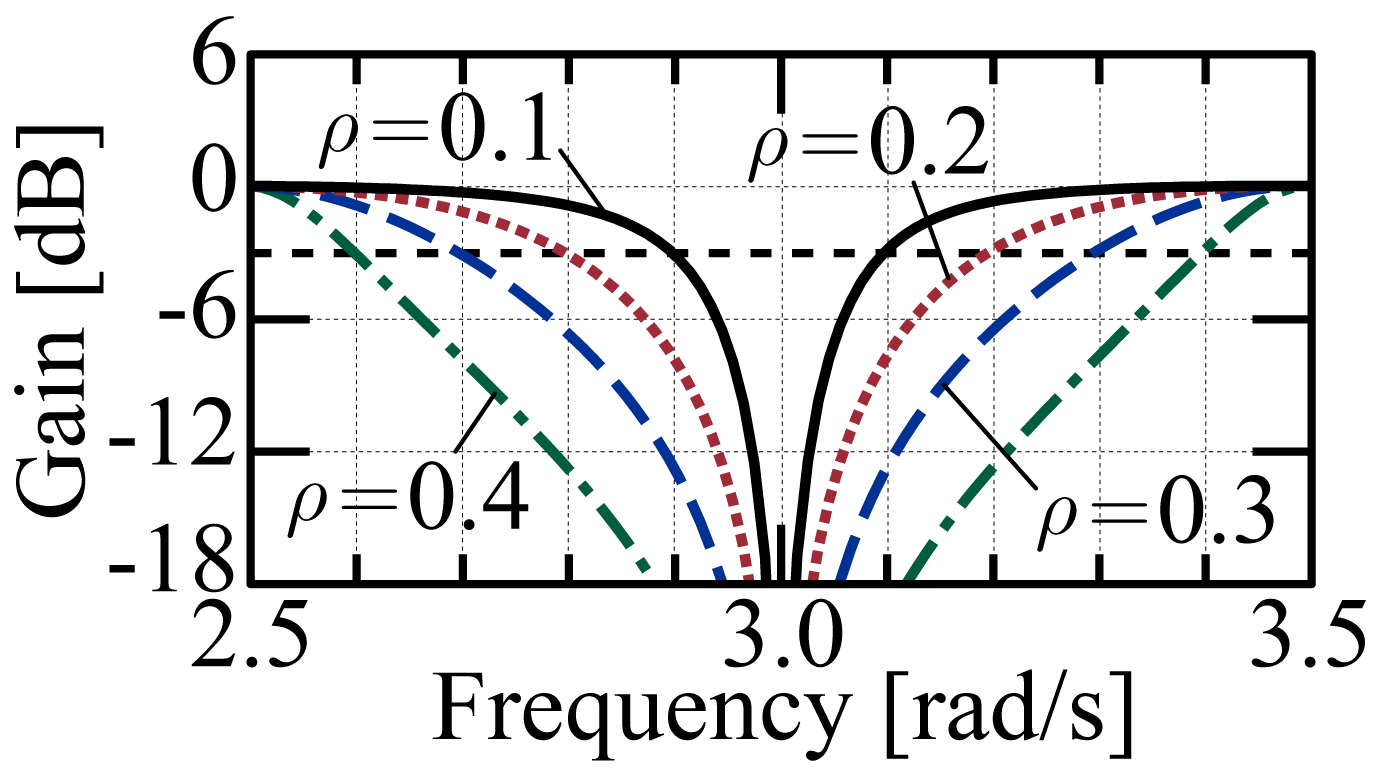
左から順に，第一高調波，第三高調波，第五高調波，第七高調波の周辺周波数特性となっている． $n\omega_0\pm \rho$の周波数でゲインが$-3$ dBとなり，高調波（周期外乱）周波数を中心とした$n\omega_0\pm \rho$の間が，準周期外乱として補償されるようになっている．そして，この分離周波数$\rho$を大きくとることにより，広帯域な高調波抑圧が実現される．この周波数特性は，先の準周期外乱の定義と辻褄が合っており，分離周波数$\rho$を変えることで準周期外乱の定義が変わり，周期外乱の周辺（ゆらぎ）のどこまでを準周期外乱として抑圧するかが変化していると理解できる．

離散時間アルゴリズム

準周期外乱オブザーバのC++サンプルプログラムは [GitHub] に公開されているので，そちらをダウンロードして利用いただきたい．擬似コードのアルゴリズムが必要であれば，論文[H. Muramatsu, IEEE TCST, 2025] に記載されている．

準周期外乱オブザーバの離散時間アルゴリズムは少し工夫して実現する必要があるため，これを紹介する．ポイントは３つであり，直接写像$e^{-Ts}\to z^{-1}$によるQフィルタの実現，後退オイラー法$s\to (1-z^{-1})/T$による厳密にプロパーでない伝達関数$B(s)P_n^{-1}(s)$の実現，Qフィルタ内部の線形位相ローパスフィルタ$\Phi(s)$を集約した実現，である．

それぞれについて簡単に説明する．まず，Qフィルタは１サンプルのむだ時間$e^{-Ts}$（$T$はサンプリングタイム）のみを用いたフィルタであり，微分項$s$や積分項$1/s$は持たない．そのため，$e^{-Ts}\to z^{-1}$で近似なく実現可能である．（言い方を変えれば，$Q(s)$は連続時間の皮を被ったデジタルフィルタとして直接設計されていた．）次に，伝達関数$B(s)P_n^{-1}(s)$は厳密にプロパーでない伝達関数であり，よく利用される双一次変換や前身オイラー法では離散時間実現できない．そのため，準周期外乱オブザーバは後退オイラー法に基づく離散時間実現を採用している．最後に，Qフィルタは複数の線形位相ローパスフィルタ$\Phi(s)$を採用しているが，それらはメモリの使用量と計算コスト重い．そのため，複数の線形位相ローパスフィルタを一箇所に集約してアルゴリズムを実現している．

ハイパーパラメータの設計

サンプルプログラム [GitHub] や [H. Muramatsu, IEEE TCST, 2025] に掲載されている準周期外乱オブザーバは公称プラント$1/(Ms^2)$を対象として，実現された離散時間アルゴリズムである．このとき，準周期外乱オブザーバは９つのパラメータをもつ．数は少し多いが，いずれも設計指針が明確に決まっており，設計・チューニングはそこまで難しくはない．それぞれのパラメータについて説明する．

$\mu\in\{0,1\}$は準周期外乱オブザーバのスイッチであり，ここで初めて登場するパラメータである．$\mu=0$でスイッチがオフとなり，補償なし・推定のみで準周期外乱オブザーバを利用できる．$\mu=1$でスイッチがオンとなり，準周期外乱オブザーバが準周期外乱を補償する．

$l,\ N_{\mathrm{max}}\in \mathbb{Z}_{>0}$は準周期外乱オブザーバの線形位相ローパスフィルタ$\Phi(s)$のハイパーパラメータである．$l$は多段で構成されるフィルタの段数を，$N_{\mathrm{max}}$は各段におけるフィルタの次数の最大数を決める．いずれも，大きくすることでフィルタのゲインが理想的なローパスフィルタに近づくが，相応に計算量が増えるトレードオフがある．経験的には，$l$は１桁の小さな値，$N_{\mathrm{max}}$は２〜３桁の大きな値にしておけば，十分な精度のフィルタが構築できる．計算量については，各実装媒体の仕様と合わせて検討されたい．

カットオフ周波数$\omega_{\mathrm{a}},\ \omega_{\mathrm{b}}\in \mathbb{R}_{>0}$は，必ず$\omega_{\mathrm{a}} \ll \omega_{\mathrm{b}}$を満たさなければならない．その上で，$\omega_{\mathrm{a}}$は補償したい高調波周波数より高く設計し，$\omega_{\mathrm{b}}$は安定化したい周波数領域より低く設計する．すなわち，準周期外乱抑圧（大きい$\omega_{\mathrm{a}}$）とロバスト安定化（小さい$\omega_{\mathrm{b}}$）は$\omega_{\mathrm{a}} \ll \omega_{\mathrm{b}}$の制約の下にトレードオフの関係にある．

分離周波数$\rho\in(0,\pi/L)$は，準周期外乱モデルもしくは，感度関数が抑圧する高調波周波数の周辺帯域の設計要求から決める．

$L,\ M,\ T\in\mathbb{R}_{>0}$は準周期外乱の周期，プラントの質量，制御器のサンプリングタイム，の同定値を利用する．

準周期外乱オブザーバの学術的貢献

最後に，従来研究を踏まえた準周期外乱オブザーバの学術的立ち位置と貢献について簡単に説明する．従来，繰り返し制御や周期外乱オブザーバなど，周期外乱抑圧手法は多数提案されてきた．それら手法は「広帯域高調波抑圧」，「非周期外乱の非増幅」，「高調波抑圧周波数の非逸脱」を同時に実現することが出来ておらず，そこにトレードオフが生じていた．準周期外乱オブザーバはこのトレードオフを解消し，それら３つの同時実現に成功した．これが準周期外乱オブザーバの学術的貢献である．

この同時実現は，準周期外乱オブザーバの一巡伝達関数の位相遅れがナイキスト周波数以下で$-90$ degに抑えられているため，制御帯域でウォーターベッド効果が回避され，達成されたと仮説立てている．準周期外乱オブザーバに現れるウォーターベッド効果については，今後の研究で詳細を明らかにする予定である．

なお，村松が過去に提案した周期外乱オブザーバ（[H. Muramatsu and S. Katsura, IEEE Trans. on Ind. Inf., 2018] ）に対しては，論文[H. Muramatsu, IEEE TCST, 2025] の準周期外乱オブザーバが完全な上位互換である．

産業応用

準周期外乱や高調波といった問題は機械および電気のあらゆる産業機器で生じる問題であり，村松は「準周期外乱オブザーバ」の産業実装を目指しています．準周期外乱オブザーバは対象とする機器を限定しない制御理論として確立されており，幅広い産業機器への応用が期待できます．本技術に関する共同研究・学術指導などに興味がある場合は，村松（muramatsu (at) hiroshima-u.ac.jp）までお気軽にご連絡ください．これまでのところ，村松はロボティクスを専門としており，ロボットを対象とした実験により，その有効性と実用性を検証済みです．

概要