, Hisayoshi Muramatsu

概要

本研究紹介は村松が提案した周期外乱オブザーバ[1]について解説する．特に，大枠の理解・設計・実装を助けることを目的とし，より詳細に興味がある場合は参考文献に記載する論文を読んでいただきたい．

周期外乱

産業機械をはじめ多くの繰り返し動作を行うロボットや自動機械はその周期動作と摩擦，姿勢変化，モデル化誤差により頻繁に周期外乱を誘発する．他にも，外因性の振動，トルクリップルらも周期外乱であり，これらは精度を悪化させる問題がある．周期外乱は

\begin{align} f_{\mathrm{p}}(t) = f_{\mathrm{p}}(t-T) \end{align}

および以下のフーリエ級数によって表すことができ，必ずしも単一周波数のみを有する正弦波や余弦波である必要はない．

\begin{align} x(t)=\frac{a_0}{2}+\sum_{n=1}^\infty[a_n\cos(n\omega_0t)+b_n\sin(n\omega_0t)] \end{align}

式(2)おける基本周波数$\omega_0\ [\mathrm{rad/s]}$の整数倍$n\omega_0$の周波数を有する正弦波および余弦波が高調波であり，周期外乱はそれら高調波$a_n\cos(n\omega_0t)+b_n\sin(n\omega_0t)$および定数項$a_0/2$を有しうり，これらを補償しなければならない．

サーボモデル

以下の運動方程式でモデル化されるようなサーボシステムを考える．

\begin{align} M\ddot{x} + C\dot{x} + Kx = f+f_{\mathrm{e}} \end{align}

$f$はサーボモータの力（トルク）であり，$f_{\mathrm{e}}$は外力である．周期外乱オブザーバを構築するにあたり，公称質量$M_{\mathrm{n}}$を用いる．公称質量と実際の質量$M$の間には以下のようにモデル化誤差$\Delta M$が存在する．

\begin{align} M=M_{\mathrm{n}} + \Delta M \end{align}

周期外乱オブザーバに限らず，外乱オブザーバにおいては式(3)を変形し，

\begin{align} M_{\mathrm{n}}\ddot{x} = f+f_{\mathrm{e}} - \Delta M \ddot{x} - C\dot{x} - Kx \end{align}

とし，右辺2–5項をまとめて外乱$f_{\mathrm{p}}$として定義し，

\begin{align} f_{\mathrm{p}} \triangleq f_{\mathrm{e}} - \Delta M \ddot{x} - C\dot{x} - Kx \end{align}

運動方程式は以下となる．

\begin{align} M_{\mathrm{n}}\ddot{x} = f + f_{\mathrm{p}} \end{align}

そして，式(7)における外乱$f_{\mathrm{p}}$が式(1)を満たすような周期外乱であると仮定する．

周期外乱オブザーバ

周期外乱オブザーバのブロック線図を図１に示す．

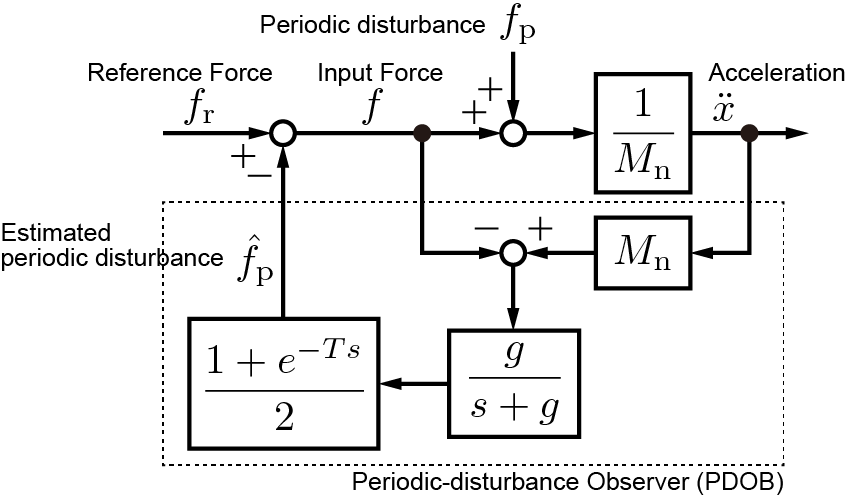
図１．周期外乱オブザーバ．

加速度に公称質量をかけて算出した力$M_{\mathrm{n}}\ddot{x}$からモータへの入力$f$を引くことにより外乱に相当する力を推定している．さらに，安定性を高めるローパスフィルタ

\begin{align} \frac{g}{s+g}\notag \end{align}

および周期外乱を抽出するコムフィルタ

\begin{align} \frac{1+e^{-Ts}}{2}\notag \end{align}

を通して推定周期外乱$\hat{f}_{\mathrm{p}}$を得る．推定周期外乱$\hat{f}_{\mathrm{p}}$およびモータに実現したい参照力$f_{\mathrm{r}}$を用いてモータへの入力$f$を決定する．

\begin{align} f=f_{\mathrm{r}}-\hat{f}_{\mathrm{p}} \end{align}

ここで，推定周期外乱$\hat{f}_{\mathrm{p}}$をフィードバックすることにより周期外乱$f_{\mathrm{p}}$を打ち消している．さらに，図１のブロック線図は図２のように等価変形できる．

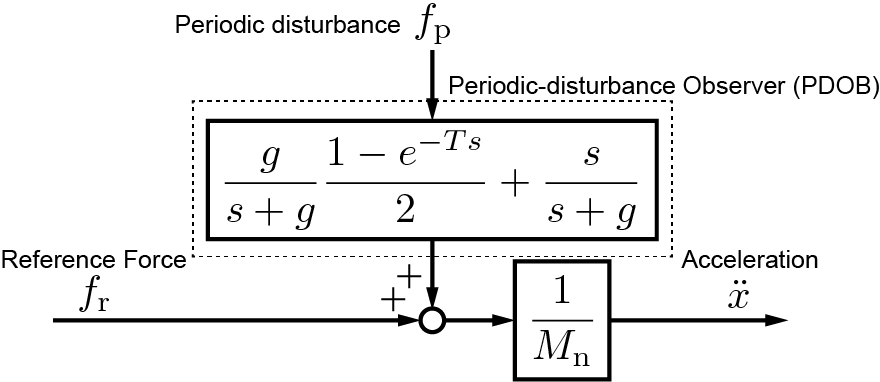
図２．周期外乱オブザーバの実装．

これより，周期外乱オブザーバは周期外乱に対して$\frac{g}{s+g}\frac{1-e^{-Ts}}{2}+\frac{s}{s+g}$のフィルタ特性を有し，加速度応答は以下のように表せる．

\begin{align} \ddot{X}(s) = \frac{1}{M_{\mathrm{n}}}F_{\mathrm{r}}(s)+\frac{1}{M_{\mathrm{n}}}\left(\frac{g}{s+g}\frac{1-e^{-Ts}}{2}+\frac{s}{s+g}\right)F_{\mathrm{p}}(s) \end{align}

周波数特性

周期外乱オブザーバの外乱抑圧特性$\frac{g}{s+g}\frac{1-e^{-Ts}}{2}+\frac{s}{s+g}$の周波数応答（ボード線図）を図３に示す．

図３．周期外乱オブザーバの外乱抑圧特性．基本周波数：$100\ \mathrm{rad/s}$．

基本周波数$100\ \mathrm{rad/s}$およびその高調波周波数$200,\ 300,\ \ldots$においてゲインが下がっていることが確認できる．これにより，基本波および高調波の抑圧が可能である．安定性が許す範囲においてローパスフィルタのカットオフ周波数$g$を高くすることにより，高い周波数帯域においてもゲインを小さく保つことが可能となる．

実装

モータに位置エンコーダが取り付けられている場合，図４のように周期外乱オブザーバを構成する．

図４．周期外乱オブザーバの実装．

速度を計算する擬似微分のカットオフ周波数$g_{\mathrm{d}}$が十分に大きい場合，上述の周波数特性を周期外乱オブザーバは実現可能である．周期外乱オブザーバのサンプルC++プログラムはhttps://github.com/HisayoshiMuramatsu/PDOBよりダウンロードできる．

発展

リアルタイムに周期を推定可能な適応ノッチフィルタと組み合わせることで，周期外乱の周期が変化するような周波数変動周期外乱を推定・補償可能な適応周期外乱オブザーバへ発展可能である[1]．適応周期外乱オブザーバのサンプルC++プログラムはhttps://github.com/HisayoshiMuramatsu/APDOBよりダウンロードできる．

また，周期外乱オブザーバと従来の外乱オブザーバを組み合わせることにより，周期外乱のみならず非周期外乱もまた補償可能なエンハンスド周期外乱オブザーバが構築可能である[2]．

応用

周期外乱オブザーバはロボットおよび産業機械の精密制御に応用可能である．周期外乱オブザーバに関する質問・学術指導・共同研究などに興味がある場合は村松（muramatsu (at) hiroshima-u.ac.jp）までお気軽にご連絡ください．

参考文献

[1] Hisayoshi Muramatsu and Seiichiro Katsura, “An Adaptive Periodic-Disturbance Observer for Periodic-Disturbance Suppression,” IEEE Transactions on Industrial Informatics, vol. 14, no. 10, pp. 4446–4456, Oct. 2018.

[IEEE Xplore], [arXiv (Open Access)], [DOI: 10.1109/TII.2018.2804338], [Research Gate],

BibTex

@ARTICLE{8288655,
author={Muramatsu, Hisayoshi and Katsura, Seiichiro},
journal={IEEE Transactions on Industrial Informatics},
title={An Adaptive Periodic-Disturbance Observer for Periodic-Disturbance Suppression},
year={2018},
volume={14},
number={10},
pages={4446-4456},
month=Oct,}

概要紹介

周期外乱を推定・補償する周期外乱オブザーバを最初に提案した論文．従来，ローパスフィルタが用いられてきた外乱オブザーバのQフィルタへむだ時間を利用し，複数の高調波を含む周期外乱の推定・補償に成功した．周期外乱オブザーバの感度関数（外乱抑圧特性）は多数のバンドストップ特性を有し，高調波を補償する．周期外乱オブザーバは従来の繰り返し制御に比べ安定性が高く，むだ時間は公称安定性に影響を与えず，相補感度関数のゲインにもピークを生じない．加えて，適応ノッチフィルタを用いた周期外乱周波数推定を行い，周期が変動する周期外乱もまた抑圧可能な適応周期外乱オブザーバを提案した．

[2] Hisayoshi Muramatsu and Seiichiro Katsura, “An Enhanced Periodic-Disturbance Observer for Improving Aperiodic-Disturbance Suppression Performance,” IEEJ Journal of Industry Applications, vol. 8, no. 2, pp. 177–184, May 2019.

[J-STAGE (Open Access)], [DOI: 10.1541/ieejjia.8.177], [Research Gate],

BibTex

@article{Hisayoshi_Muramatsu2019,
title={An Enhanced Periodic-Disturbance Observer for Improving Aperiodic-Disturbance Suppression Performance},
author={Hisayoshi Muramatsu and Seiichiro Katsura},
journal={IEEJ Journal of Industry Applications},
volume={8},
number={2},
pages={177-184},
year={2019},
month=Mar,}

概要紹介

[2]の周期外乱オブザーバを発展させた研究．周期外乱オブザーバは周期外乱の推定・補償が可能な一方で，現実には多くの非周期外乱も存在し，これもまた補償する必要がある．このため，周期外乱オブザーバと従来の外乱オブザーバを組み合わせ，周期外乱と非周期外乱の双方を推定・補償可能な強化周期外乱オブザーバを提案した．組み合わされた従来の外乱オブザーバにより非周期外乱の推定・補償が実現した．

[3] Xiao Feng, Hisayoshi Muramatsu, and Seiichiro Katsura, “Differential Evolutionary Algorithm with Local Search for the Adaptive Periodic-Disturbance Observer Adjustment,” IEEE Transactions on Industrial Electronics, vol. 68, no. 12, pp. 12504–12512, Dec. 2021.

[IEEE Xplore], [DOI: 10.1109/TIE.2020.3040664], [Research Gate],

BibTex

@ARTICLE{9280360,
author={Feng, Xiao and Muramatsu, Hisayoshi and Katsura, Seiichiro},
journal={IEEE Transactions on Industrial Electronics},
title={Differential Evolutionary Algorithm With Local Search for the Adaptive Periodic-Disturbance Observer Adjustment},
year={2021},
volume={68},
number={12},
pages={12504-12512},
month=Dec,}

概要紹介

[2]で提案した適応周期外乱オブザーバにおける非線形に関係する複雑なパラメータの設計を，進化アルゴリズムを用いることで自動化および最適化することに成功した．人間が試行錯誤的に設計していたところを自動・最適化することで，適応周期外乱オブザーバがより良い性能を設計者によらず発揮できるになった．